Motivation

Focal loss (FL) was introduced by Tsung-Yi Lin et al., in their 2018 paper “Focal Loss for Dense Object Detection”.1 Given an image, the object detection algorithms usually have to propose a good number of regions in which potential objects might sit. In R-CNN and Fast R-CNN algorithms, the number of regions proposed is limited intentionally to several thousand. In Faster R-CNN models and other models with CNN region proposal mechanisms, the number of regions proposed could be as high as several hundred thousand. Of course, most of the regions proposed are negative examples where there is no object inside. In R-CNN and Fast R-CNN, because the model is not end-to-end but rather consists of several distinct models, the class imbalanced problem could be solved by sampling more minor class samples or removing major class samples.

However, in state of the art object detection models beginning with Faster R-CNN, the authors believed that the extreme foreground-background class imbalance hinders the first-stage detector from achieving a better performance, where balanced sampling cannot be easily implemented. As such, FL is designed to address scenarios with extreme imbalanced classes, such as one-stage object detection where the imbalance between foreground and background classes can be, for example, 1:1000.

Solution

Therefore, they improve the traditional cross entropy (CE) loss function and devise Focal Loss (FL), which focuses training on hard examples, avoiding the vast number of easy negative examples from overwhelming the detector during training. Hard example here refers to the examples in the training set that are poorly predicted, i.e. being mislabeled by the current version of the classifier. Easy example is exactly the opposite.

How it Works

The default loss function for most classification tasks is CE:

CE(p,y)=−(ylogp+(1−y)log(1−p))(1)\text{CE}(p, y) = -(y\text{log}p + (1-y)\text{log}(1-p)) \tag{1}

Adding a modulating factor related to $p$ and $\gamma$ and a balanced factor $\alpha$ to CE, FL is obtained as follows:

FL(p,y)=−(αy+(1−α)(1−y))⋅((1−(yp+(1−y)(1−p)))γ)⋅(ylogp+(1−y)log(1−p))(2)\text{FL}(p, y) = -(\alpha y + (1-\alpha)(1-y)) \cdot ((1-(yp + (1-y)(1-p)))^\gamma) \cdot (y\text{log}p + (1-y)\text{log}(1-p)) \tag{2}

Or more compactly:

FL(y,p)=−yα(1−p)γlog(p)−(1−y)(1−α)pγlog(1−p)(3)FL(y, p) = -y\alpha(1-p)^\gamma \text{log}(p) - (1-y)(1-\alpha)p^\gamma \text{log}(1-p) \tag{3} FL(pt)=−αt(1−pt)γlog(pt)(4)\text{FL}(p_t) = -\alpha_t(1-p_t)^\gamma log(p_t) \tag{4}

where $y \in [0, 1]$ is the ground truth label, $p_{t}\in [0,1]$ is the model’s predicted probability for the class with label $y=1$, and $\alpha_t$ is defined as:

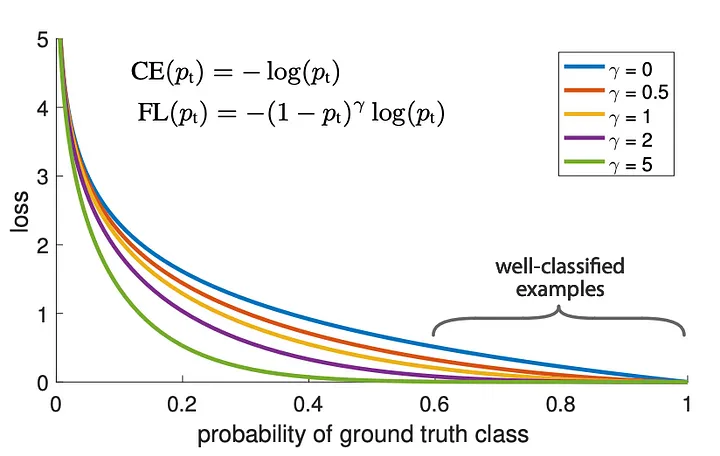
αt={α∈[0,1]if y=11−αotherwise\alpha_t = \left\{\begin{matrix} \alpha \in [0, 1]& \text{if } y=1 \\ 1-\alpha & \text{otherwise} \end{matrix}\right. So we are adding the weight term $\alpha_{t}(1-p_t)^\gamma$ in addition to the cross entropy loss. So when $\gamma$ is 0 then FL is simply the cross entropy loss. As $\gamma$ increases, the focal loss values of easy examples ($p_{t}> 0.5$) are reduced, while hard examples (where $p_{t}« 0.5$) are reduced to a maximum of one quarter, making the classifier concentrate on hard samples. Quoting from the authors: 

“with $\gamma$ = 2, an example classified with $p_t$ = 0.9 would have 100 × lower loss compared with CE and with $p_t$ ≈ 0.968 it would have 1000 × lower loss.””

So as the confidence of the classification increases, ie. the probability of ground truth cases, samples are considered increasingly “easier” and contribute less and less to the loss. The result is that the hard examples, or where the probability of ground truth is lower, contribute the most to the loss, thus forcing the model to tend to them in order to minimize the loss function. This is conceptually similar to boosting algorithms, where previously incorrectly classified examples receive more weight but in a different context.

Using FL as an Optimizer

For binary classification tasks, assume the prediction output of our model is pred. Then the corresponding probability is sigmoid(pred) or s(pred) for short. Substituting for $p$ into (2) above we get our evaluation function:

FL(pred,y)=−(αy+(1−α)(1−y))⋅((1−(y⋅s(pred)+(1−y)(1−s(pred))))γ)⋅(ylog(s(pred))+(1−y)log(1−s(pred)))(5)\text{FL}(pred, y) = -(\alpha y + (1-\alpha)(1-y)) \cdot ((1-(y\cdot s(pred) + (1-y)(1-s(pred))))^\gamma) \cdot (y\text{log}(s(pred)) + (1-y)\text{log}(1-s(pred))) \tag{5}

All that is left to optimize according to FL is to calculate the first-order and second-order partial derivative of $\text{FL}(pred, y)$ with respect to pred and take them as the return value of objective loss function.

FL Gradient

Luckily for us, the authors of the paper provide the derivative of focal loss with respect to the model’s output $z$ in appendix B:

∂FL∂z=αty(1−pt)γ(γptlog(pt)+pt−1)(6)\frac{\partial FL}{\partial z} = \alpha_ty(1-p_t)^\gamma (\gamma p_t \text{log}(p_t) +p_t -1) \tag{6}

But lets try deriving it anyway. So we want to use the chain rule to solve:

∂FL∂z=∂FL∂pt∂pt∂p∂p∂z(7)\frac{\partial FL}{\partial z} = \frac{\partial FL}{\partial p_t}\frac{\partial p_t}{\partial p}\frac{\partial p}{\partial z} \tag{7}

So solving each component one at a time we get for the first term:

∂FL∂pt=αtγ(1−pt)γ−1log(pt)−αt(1−pt)γpt(8)\frac{\partial FL}{\partial p_{t}}= \alpha_t\gamma(1-p_t)^{\gamma-1}\text{log}(p_{t)-}\frac{\alpha_{t}(1-p_{t})^\gamma}{p_t} \tag{8}

The second component $\frac{\partial p_t}{\partial p}$ relies on the relationship:

pt=p(y+1)2+(1−p)(1−y)2p_{t}= \frac{p(y+1)}{2} + \frac{(1-p)(1-y)}{2}

So our derivative is

∂pt∂p=y+12+y−12=y(9)\frac{\partial p_t}{\partial p} = \frac{y+1}{2} + \frac{y-1}{2} = y \tag{9}

Our third term is the derivative of a sigmoid function $p(z) = \frac{1}{1+e^{-z}}$ which is just:

∂p∂z=p(1−p)(10)\frac{\partial p}{\partial z} = p(1-p) \tag{10}

Since $p(1-p)$ is equal to $p_t(1-p_t)$ some terms cancel out and we are left with equation (6).

FL Hessian

We can obtain the second order derivative by differentiating the gradient we have obtained (6) with respect to $z$:

∂2FL∂z2=∂∂z(∂FL∂z)\frac{\partial^2 FL}{\partial z^2} = \frac{\partial }{\partial z}(\frac{\partial FL}{\partial z}) =∂∂pt(∂FL∂z)×∂pt∂p×∂p∂z(11)= \frac{\partial }{\partial p_t}(\frac{\partial FL}{\partial z}) \times \frac{\partial p_t}{\partial p} \times \frac{\partial p}{\partial z} \tag{11}

We have already computed the last two elements of the chain ($y$ and $p(1-p)$ respectfully), so we just have to compute the first element of the chain. We will use the following notation to make our computations a bit cleaner: $\frac{\partial FL}{\partial z} = u \times v$ where $u = \alpha_{t}y(1-p_t)^\gamma$ and $v = \gamma p_t\text{log}(p_{t)}+ p_{t}-1$

Now we compute the derivatives of $u$ and $v$ with respect to $p_t$:

∂u∂pt=−γαty(1−pt)γ−1(12)\frac{\partial u}{\partial p_{t}}= -\gamma \alpha_ty(1-p_t)^{\gamma-1} \tag{12} ∂v∂pt=γlog(pt)+γ+1(13)\frac{\partial v}{\partial p_{t}}= \gamma \text{log}(p_{t)}+ \gamma + 1 \tag{13}

So our second order derivative, or Hessian, is:

∂2FL∂z2=(∂u∂pt×v+u×∂v∂pt)×∂pt∂p×∂p∂z(14)\frac{\partial^2 FL}{\partial z^2} = (\frac{\partial u}{\partial p_t} \times v + u \times \frac{\partial v}{\partial p_t}) \times \frac{\partial p_t}{\partial p} \times \frac{\partial p}{\partial z} \tag{14}

Coding FL

Focal loss was initially proposed to resolve the imbalance issues that occur when training object detection models. However, it can and has been used for many imbalanced learning problems. Focal loss is just a loss function, and may thus be used in conjunction with any model that uses gradients, including neural networks and gradient boosting.

To code any loss function in a ML/DL setting, we need the loss expressed mathematically as well as its gradient and hessian (the first and second order derivatives). Here, we will use LightGBM/Catboost, since one of their nice features is that you can provide it with a custom loss function.

As your optimization function:

def focal_loss_lgb(y_pred, dtrain, alpha, gamma):
  a,g = alpha, gamma
  y_true = dtrain.label
  def fl(x,t):
  	p = 1/(1+np.exp(-x))
  	return -( a*t + (1-a)*(1-t) ) * (( 1 - ( t*p + (1-t)*(1-p)) )**g) * ( t*np.log(p)+(1-t)*np.log(1-p) )
  partial_fl = lambda x: fl(x, y_true)
  grad = derivative(partial_fl, y_pred, n=1, dx=1e-6)
  hess = derivative(partial_fl, y_pred, n=2, dx=1e-6)
  return grad, hess

As your evaluation function (as opposed to F1 score):

def focal_loss_lgb_eval_error(y_pred, dtrain, alpha, gamma):
  a,g = alpha, gamma
  y_true = dtrain.label
  p = 1/(1+np.exp(-y_pred))
  loss = -( a*y_true + (1-a)*(1-y_true) ) * (( 1 - ( y_true*p + (1-y_true)*(1-p)) )**g) * ( y_true*np.log(p)+(1-y_true)*np.log(1-p) )
  # (eval_name, eval_result, is_higher_better)
  return 'focal_loss', np.mean(loss), False

A more modular/cleaner approach might look like this, courtesy of Max Halford2:

```python
import numpy as np
from scipy import optimize
from scipy import special

class FocalLoss:

    def __init__(self, gamma, alpha=None):
        self.alpha = alpha
        self.gamma = gamma

    def at(self, y):
        if self.alpha is None:
            return np.ones_like(y)
        return np.where(y, self.alpha, 1 - self.alpha)

    def pt(self, y, p):
        p = np.clip(p, 1e-15, 1 - 1e-15)
        return np.where(y, p, 1 - p)

    def __call__(self, y_true, y_pred):
        at = self.at(y_true)
        pt = self.pt(y_true, y_pred)
        return -at * (1 - pt) ** self.gamma * np.log(pt)

    def grad(self, y_true, y_pred):
        y = 2 * y_true - 1  # {0, 1} -> {-1, 1}
        at = self.at(y_true)
        pt = self.pt(y_true, y_pred)
        g = self.gamma
        return at * y * (1 - pt) ** g * (g * pt * np.log(pt) + pt - 1)

    def hess(self, y_true, y_pred):
        y = 2 * y_true - 1  # {0, 1} -> {-1, 1}
        at = self.at(y_true)
        pt = self.pt(y_true, y_pred)
        g = self.gamma

        u = at * y * (1 - pt) ** g
        du = -at * y * g * (1 - pt) ** (g - 1)
        v = g * pt * np.log(pt) + pt - 1
        dv = g * np.log(pt) + g + 1

        return (du * v + u * dv) * y * (pt * (1 - pt))

    def init_score(self, y_true):
        res = optimize.minimize_scalar(
            lambda p: self(y_true, p).sum(),
            bounds=(0, 1),
            method='bounded'
        )
        p = res.x
        log_odds = np.log(p / (1 - p))
        return log_odds

    def lgb_obj(self, preds, train_data):
        y = train_data.get_label()
        p = special.expit(preds)
        return self.grad(y, p), self.hess(y, p)

    def lgb_eval(self, preds, train_data):
        y = train_data.get_label()
        p = special.expit(preds)
        is_higher_better = False
        return 'focal_loss', self(y, p).mean(), is_higher_better

``

  1. T.-Y. Lin, P. Goyal, R. Girshick, K. He, and P. Dollar, “Focal loss ´ for dense object detection,” in Proceedings of the IEEE international conference on computer vision, 2017, pp. 2980–2988. ↩

  2. https://maxhalford.github.io/blog/lightgbm-focal-loss/ ↩