Introduction

With the rapid increase of large-scale, real-world datasets, it becomes critical to address the problem of long-tailed data distribution (i.e., a few classes account for most of the data, while most classes are under-represented). Solutions have typically adopted class re-balancing strategies such as re-sampling and re-weighting based on the number of observations for each class. Many boosting algorithms that were part of the machine learning boom back 2016-17, which are natural fits for dealing with class imbalances due to their role as ensembles of weak learners, have hyperparameters related to class weights.

So from my perspective, with the initial ML boon in the mid to late 2020s, you had two methods available to you to deal with class imbalances that so often occur in industry: data-level methods and algorithm-level methods.

Data-Level Methods

Data-level methods alter the class distribution in the original data by employing re-sampling strategies to balance the dataset. The simplest forms of resampling include random over-sampling and random undersampling. The former, like the Synthetic Minority Oversampling Technique (SMOTE) for example, handles class imbalance by duplicating the instances in the rare minority class and thus, augmenting the minority class, whereas the latter randomly drops instances from the majority class to match the cardinality of minority class. Experiments suggest that data sampling strategies have little effect on classification performance, however, other results in demonstrate that random oversampling leads to performance improvements.1

While sampling strategies are widely adopted, these methods manipulate the original class representation of the given domain and introduce drawbacks. Particularly, over-sampling can potentially lead to overfitting and may aggravate the computational burden while under-sampling may eliminate useful information that could be vital for the induction process. For example, Castro et al. demonstrates that strategies adopted to mitigate effects of class imbalance such as undersampling adversely affect probability calibration of minority classes.2 Moreover, a classifier developed by employing sampling methods to artificially balance data may not be applicable to a population with a much difference prevalence rate since the classifier is trained to perform well on balanced data.

Algorithm-Level Methods

Algorithm-level approach involve adjusting the classifier, and can further be categorized into ensemble methods and cost-sensitive methods. The most widely used methods include bagging and boosting ensemble-based methods. For example, with XGBoost, scale_pos_weight value is used to scale the gradient for the positive class. This has the effect of scaling errors made by the model during training on the positive class and encourages the model to over-correct them. In turn, this can help the model achieve better performance when making predictions on the positive class. Pushed too far, it may result in the model overfitting the positive class at the cost of worse performance on the negative class or both classes. As such, the scale_pos_weight can be used to train a class-weighted or cost-sensitive version of XGBoost for imbalanced classification.

A sensible default value to set for the scale_pos_weight hyperparameter is the inverse of the class distribution. For example, for a dataset with a 1 to 100 ratio for examples in the minority to majority classes, the scale_pos_weight can be set to 100. This will give classification errors made by the model on the minority class (positive class) 100 times more impact, and in turn, 100 times more correction than errors made on the majority class. The XGBoost documentation suggests a fast way to estimate this value using the training dataset as the total number of examples in the majority class divided by the total number of examples in the minority class: scale_pos_weight = total_negative_examples / total_positive_examples.

A New Set of Tools Emerges: Optimization-Level Methods

As the ML boom of the mid 2010s turned into the DL revolution of the late 2010s and early 2020s, synergies began to emerge across different subject areas and frameworks. Knowledge and practices invented for DL could be applied to ML settings, while theoretical knowledge gained from the study of ML systems like gradient behaviors could be used to inform the early theoretical work being done on DL. In the theme of our current topic of class imbalance, unique approaches were being developed for specific issues that could simultaneously be applied to a range of problems. For example, I have written in a previous post about Focal Loss, originally designed to solve object detection problems in a computer vision setting. This loss function was quickly applied to other areas to address the common occurrence of class imbalances in binary classification.

These approaches were being developed for deep learning frameworks in the binary classification setting, often manipulating the cross-entropy loss that has become the de-facto loss function for deep binary classification tasks. Although not new from a theoretical or statistical perspective (a class-balanced loss assigns sample weights inversely proportionally to the class frequency3), cost sensitive learning methods seek to reinforce the sensitivity of the classification algorithm towards the under-represented class by building on advancements in ML/DL by incorporating class-wise costs into the objective function of the classification algorithm during training process. So instead of each instance being either correctly or incorrectly classified, each class (or instance) is given a misclassification cost. Thus, instead of trying to optimize the accuracy, the problem is then to minimize the total misclassification cost.

So building off my earlier post about Focal Loss, I would like to present another work that was published around the same time at Google. Like the Focal Loss paper, this novel paper seeks to address a specific issue in DL, but provides a tool that is applicable to any practitioner involves in classification tasks.

Class-Balanced Loss Based on Effective Number of Samples

In a single sentence, proposes a class-wise re-weighting scheme for most frequently used losses (softmax-cross-entropy, focal loss, etc.) giving a quick boost of accuracy, especially when working with data that is highly class imbalanced.4 Their Class-Balanced Loss is designed to address the problem of training from imbalanced data by introducing a weighting factor that is inversely proportional to the effective number of samples. The class-balanced loss term can be applied to a wide range of deep networks and loss functions.

The authors begin the paper by noting that in the context of deep feature representation learning using CNNs, re-sampling may either introduce large amounts of duplicated samples, which slows down the training and makes the model susceptible to overfitting when oversampling, or discard valuable examples that are important for feature learning when under-sampling. I have also found this to be in the case with other neural network architectures as well as gradient-boosting algorithms. Due to these disadvantages of applying re-sampling for CNN training, the authors focus on re-weighting approaches, namely, how to design a better class-balanced loss.

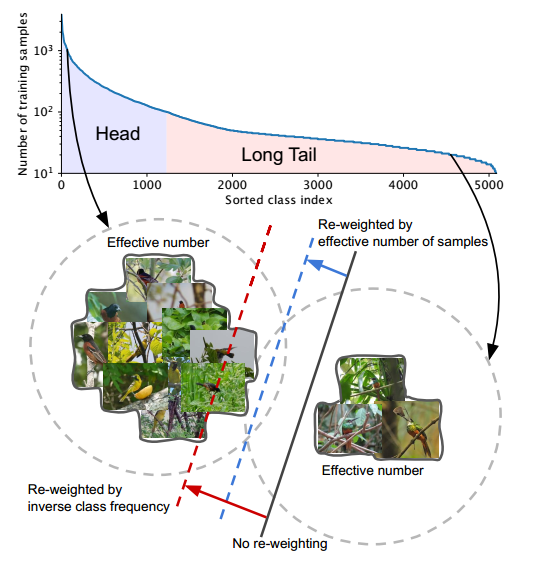
Due to highly imbalanced data, directly training the model or re-weighting the loss by inverse number of samples cannot yield satisfactory performance. Intuitively, the more data, the better. However, since there is information overlap among data, as the number of samples increases, the marginal benefit a model can extract from the data diminishes.

In light of this, the authors propose a novel theoretical framework to characterize data overlap and calculate the effective number of samples in a model and loss-agnostic manner. A class-balanced re-weighting term that is inversely proportional to the effective number of samples is added to the loss function. Extensive experimental results indicate that this class-balanced term provides a significant boost to the performance of commonly used loss functions for training CNNs on long-tailed datasets.

Their theoretical framework is inspired by the random covering problem, where the goal is to cover a large set by a sequence of i.i.d. random small sets. The idea is to capture the diminishing marginal benefits by using more data points of a class. Due to intrinsic similarities among real-world data, as the number of samples grows, it is highly possible that a newly added sample is a near-duplicate of existing samples.

Data Sampling as Random Covering

Given a class, denote the set of all possible data in the feature space of the class as $S$. The volume of $S$ is $N$ and $N \geq 1$. The data sampling process is a random covering problem where the more data being sampled, the better the coverage of $S$. The expected total volume of sampled data increases as the number of data increases and is bounded by $N$.

Therefore, the authors define what they call the effective number of samples as an exponential function of the number of samples. with a hyperparameter $\beta \in [0, 1)$ controlling how fast the expected volume of samples grows. This expected volume of samples is denoted as the effective number of samples $E_n$, where $n$ is the number of samples, and can be defined as follows:

En=(1−βn)1−β=∑j=1nβj−1(1)E_n = \frac{(1-\beta^n)}{1-\beta} = \sum_{j=1}^n \beta^{j-1} \tag{1}

This means that the $j^{th}$ sample contributes $\beta^{j-1}$ to the effective number. The total volume N for all possible data in the class can then be calculated as:

N=lim⁡n→∞∑j=1nβj−1=11−β(2)N = \lim_{n\rightarrow \infty} \sum_{j=1}^n \beta^{j-1} = \frac{1}{1-\beta} \tag{2}

How it Works in Practice

For an input sample $x$ with label $y \in {1, 2, 3, …, C}$ where $C$ is the total number of classes, the loss of the model can be denoted as $L(p, y)$ where $p \in [0, 1]$ are the estimated class probabilities $p = [p_{1}, p_{2}, …, p_{C}]^T$. Supposing the number of samples for class $i$ is $n_i$, based on (1) then the number of samples for class $i$ is

Eni=1−βini1−βi(3)E_{n_{i}}= \frac{1-\beta_i^{n_i}}{1-\beta_{i}} \tag{3}

where $\beta_{i} = \frac{N_{i}- 1}{N_i}$. To balance the loss, a normalized weighting factor $\alpha_i$ is introduced that is inversely proportional to the effective number of samples for class $i$: $\alpha_{i} \propto \frac{1}{E_{n_i}}$.

TLDR: given a sample from class $i$ that contains $n_i$ samples in total, the authors propose to add a weighting factor $\frac{1-\beta}{1-\beta^{n_i}}$ where $\beta \in [0, 1)$ is a hyperparameter.

Finally, the class-balanced (CB) loss can be written as:

CB(p,y)=1EnyL(p,y)=1−β1−βnyL(p,y)(4)\text{CB}(p, y) = \frac{1}{E_{n_{y}}}L(p,y) = \frac{1-\beta}{1-\beta^{n_{y}}}L(p,y) \tag{4}

where $n_i$ is the number of samples in the ground-truth class $y$. Note that $\beta=0$ corresponds to no re-weighting and $\beta \rightarrow 1$ corresponds to re-weighting by inverse class frequency. The proposed novel concept of effective number of samples enables us to use a hyperparameter $\beta$ to smoothly adjust the class-balanced term between no re-weighting and re-weighing by inverse class frequency.

Applications

The proposed class-balanced term is model-agnostic and loss-agnostic in the sense that it’s independent to the choice of loss function and predicted class probabilities. Here is how to apply class-balanced term to two commonly used loss functions: softmax cross-entropy loss and focal loss:

CEsoftmax(z,y)=−log(exp(zy)∑j=1Cexp(zj))(5a)\text{CE}_{\text{softmax}}(z, y) = -\text{log}(\frac{\text{exp}(z_y)}{\sum_{j=1}^{C}\text{exp}(z_{j})}) \tag{5a} CBsoftmax(z,y)=−1−β1−βnylog(exp(zy)∑j=1Cexp(zj))(5b)\text{CB}_{\text{softmax}}(z, y) = -\frac{1-\beta}{1-\beta^{n_{y}}}\text{log}(\frac{\text{exp}(z_y)}{\sum_{j=1}^{C}\text{exp}(z_{j})}) \tag{5b} FL(z,y)=−∑i=1C(1−pit)γlog(pit)(6a)\text{FL}(z, y) = -\sum_{i=1}^{C}(1-p_i^t)^{\gamma}\text{log}(p_i^t) \tag{6a} CBfocal(z,y)=−1−β1−βny∑i=1C(1−pit)γlog(pit)(6a)\text{CB}_{\text{focal}}(z, y) = -\frac{1-\beta}{1-\beta^{n_{y}}}\sum_{i=1}^{C}(1-p_i^t)^{\gamma}\text{log}(p_i^t) \tag{6a}

Code Implementation

import numpy as np
import torch
import torch.nn.functional as F


def focal_loss(labels, logits, alpha, gamma):
    """Compute the focal loss between `logits` and the ground truth `labels`.

    Focal loss = -alpha_t * (1-pt)^gamma * log(pt)
    where pt is the probability of being classified to the true class.
    pt = p (if true class), otherwise pt = 1 - p. p = sigmoid(logit).

    Args:
      labels: A float tensor of size [batch, num_classes].
      logits: A float tensor of size [batch, num_classes].
      alpha: A float tensor of size [batch_size]
        specifying per-example weight for balanced cross entropy.
      gamma: A float scalar modulating loss from hard and easy examples.

    Returns:
      focal_loss: A float32 scalar representing normalized total loss.
    """    
    BCLoss = F.binary_cross_entropy_with_logits(input=logits,
											    target=labels,
											    reduction="none")

    if gamma == 0.0:
        modulator = 1.0
    else:
        modulator = torch.exp(-gamma * labels * logits - gamma * torch.log(1 + 
            torch.exp(-1.0 * logits)))

    loss = modulator * BCLoss

    weighted_loss = alpha * loss
    focal_loss = torch.sum(weighted_loss)

    focal_loss /= torch.sum(labels)
    return focal_loss


def CB_loss(labels, logits, samples_per_cls, no_of_classes, loss_type, beta, gamma):
    """Compute the Class Balanced Loss between `logits` and the ground truth `labels`.

    Class Balanced Loss: ((1-beta)/(1-beta^n))*Loss(labels, logits)
    where Loss is one of the standard losses used for Neural Networks.

    Args:
      labels: A int tensor of size [batch].
      logits: A float tensor of size [batch, no_of_classes].
      samples_per_cls: A python list of size [no_of_classes].
      no_of_classes: total number of classes. int
      loss_type: string. One of "sigmoid", "focal", "softmax".
      beta: float. Hyperparameter for Class balanced loss.
      gamma: float. Hyperparameter for Focal loss.

    Returns:
      cb_loss: A float tensor representing class balanced loss
    """
    effective_num = 1.0 - np.power(beta, samples_per_cls)
    weights = (1.0 - beta) / np.array(effective_num)
    weights = weights / np.sum(weights) * no_of_classes

    labels_one_hot = F.one_hot(labels, no_of_classes).float()

    weights = torch.tensor(weights).float()
    weights = weights.unsqueeze(0)
    weights = weights.repeat(labels_one_hot.shape[0],1) * labels_one_hot
    weights = weights.sum(1)
    weights = weights.unsqueeze(1)
    weights = weights.repeat(1,no_of_classes)

    if loss_type == "focal":
        cb_loss = focal_loss(labels_one_hot, logits, weights, gamma)
    elif loss_type == "sigmoid":
        cb_loss = F.binary_cross_entropy_with_logits(input=logits,
												    target=labels_one_hot,
												    weights=weights)
    elif loss_type == "softmax":
        pred = logits.softmax(dim = 1)
        cb_loss = F.binary_cross_entropy(input=pred,
								        target=labels_one_hot,
								        weight=weights)
    return cb_loss


no_of_classes = 5
logits = torch.rand(10,no_of_classes).float()
labels = torch.randint(0,no_of_classes, size = (10,))
beta = 0.9999
gamma = 2.0
samples_per_cls = [2,3,1,2,2]
loss_type = "focal"

cb_loss = CB_loss(labels,
				  logits,
				  samples_per_cls,
				  no_of_classes,
				  loss_type,
				  beta,
				  gamma)
print(cb_loss)

  1. M. Buda, A. Maki, and M. A. Mazurowski, “A systematic study of the class imbalance problem in convolutional neural networks,” Neural Networks, vol. 106, pp. 249–259, 2018. ↩

  2. C. L. Castro and A. P. Braga, “Novel cost-sensitive approach to improve the multilayer perceptron performance on imbalanced data,” IEEE transactions on neural networks and learning systems, vol. 24, no. 6, pp. 888–899, 2013. ↩

  3. C. Huang, Y. Li, C. Change Loy, and X. Tang. Learning deep representation for imbalanced classification. In CVPR, 2016; N. Sarafianos, X. Xu, and I. A. Kakadiaris. Deep imbalanced attribute classification using visual attention aggregation. In ECCV, 2018. ↩

  4. Yin Cui, Menglin Jia, Tsung-Yi Lin, Yang Song, & Serge J. Belongie (2019). Class-Balanced Loss Based on Effective Number of Samples_. CoRR, abs/1901.05555. ↩